統計とうけい学がくとは

統計とうけい学がくとは

集めたデータから、その傾向けいこうや性質せいしつを明らかあきらかにして、分析ぶんせきするための学問がくもんです。

例えばたとえば、日本にっぽんには1億おく2千せん万まん（120,000,000）を超えるこえる人ひとが生活せいかつしています。その全員ぜんいんの情報じょうほうを集めるあつめるために「国勢こくせい調査ちょうさ」が行われておこなわれています（全数ぜんすう調査ちょうさ）。ただし、国勢こくせい調査ちょうさを実施じっしするにはたくさんのお金おかねや人ひと手てが必要ひつようなので、5年に一度いちどしか実施じっししません。

実はじつは、全員ぜんいんを調べしらべなくても、1万人まんにん（10,000）を対象たいしょうに情報じょうほうを集めるあつめる（標本ひょうほん調査ちょうさ）ことができれば、ほぼ正確せいかくなデータを集めるあつめることができます。

いずれの調査ちょうさ方法ほうほうも統計とうけい学がくでは正しいただしいやり方やりかたとして使われています。

統計とうけい学がくの役割やくわり

• データの整理せいり：たくさんあるデータを「平均値へいきんち」や「グラフ化」によってわかりやすくします
• 傾向けいこうをみる：データの特徴とくちょうや規則きそく性せいを明らかあきらかにします
• 未来みらいの予測よそく：過去かこのデータから、近いちかい未来みらいを予測よそくします
• 関係かんけいの分析ぶんせき：複数ふくすうのデータの関係かんけいを分析ぶんせきします

統計とうけい学がくの活用かつよう例れい

• ビジネス：顧客こきゃくの分析ぶんせきや売上のうりあげの改善かいぜん、需要じゅようの予測よそく　など
• 医療いりょう：新薬しんやくの作成さくせいや病気びょうきの分析ぶんせき　など
• 日常にちじょう生活せいかつ：天気予報てんきよほう　など
• 研究けんきゅう：データを分析ぶんせきして結論けつろんを導き出すだす

データの傾向けいこうを見るみる

集めたたくさんのデータを分析ぶんせきする方法ほうほうについて勉強べんきょうしましょう。

たとえば、50人ひとのテストの点数てんすうが以下いかのようなものだったとします。

72、81、55、60、65、45、63、50、35、78、61、52、48、75、62、59、68、54、65、58、67、57、70、43、69、56、60、73、40、66、54、68、59、64、90、49、71、57、80、61、63、58、77、51、66、53、62、46、74、55

このままでは分析ぶんせきすることができません。

平均値へいきんち

平均値へいきんちとは、データの傾向けいこうをみるための方法ほうほうのひとつです。

すべてのデータを足してたして、データの数かずで割りわります。

(72＋81＋55＋60＋65＋45＋63＋50＋35＋78＋61＋52＋48＋75＋62＋59＋68＋54＋65＋58＋67＋57＋70＋43＋69＋56＋60＋73＋40＋66＋54＋68＋59＋64＋90＋49＋71＋57＋80＋61＋63＋58＋77＋51＋66＋53＋62＋46＋74＋55)÷50＝61.3

Excelでは平均値へいきんちを計算けいさんするのにAVERAGE関数かんすうを使います。

=AVERAGE(範囲はんい)

中央値ちゅうおうち

中央値ちゅうおうちとは、データの傾向けいこうをみるための方法ほうほうのひとつです。

データを大きさおおきさ順じゅんに並べてならべて、その中央ちゅうおうにある数かずです。データの数かずが奇数きすうの場合ばあいはその中心ちゅうしんの数かず、データの数かずが偶数ぐうすうの場合ばあいは中心ちゅうしんにある2つの平均へいきんの数かずです。

90、81、80、78、77、75、74、73、72、71、70、69、68、68、67、66、66、65、65、64、63、63、62、62、61、61、60、60、59、59、58、58、57、57、56、55、55、54、54、53、52、51、50、49、48、46、45、43、40、35

Excelでは中央値ちゅうおうちを計算けいさんするのにMEDIAN関数かんすうを使います。

=MEDIAN(範囲はんい)

最頻値さいひんち

最頻値さいひんちとは、データの傾向けいこうをみるための方法ほうほうのひとつです。

データでもっとも多くでてくる数かずです。同じおなじ個数こすうのデータが複数ふくすうある場合ばあいは、最初さいしょに出てきた数かずになります。

90、81、80、78、77、75、74、73、72、71、70、69、68、68、67、66、66、65、65、64、63、63、62、62、61、61、60、60、59、59、58、58、57、57、56、55、55、54、54、53、52、51、50、49、48、46、45、43、40、35

Excelでは最頻値さいひんちを計算けいさんするのにMODE.SNGL関数かんすうを使います。

=MODE.SNGL(範囲はんい)

度数どすう分布ぶんぷ表ひょう

データを値あたいごとに分けわけて、その傾向けいこうをみるための表ひょうを作成さくせいします。

階級かいきゅう（データを区切るくぎる範囲はんい）	度数どすう（該当がいとうするデータ数かず）
35以上いじょう45未満みまん	4
45以上いじょう55未満みまん	11
55以上いじょう65未満みまん	18
65以上いじょう75未満みまん	12
75以上いじょう85未満みまん	4
85以上いじょう	1

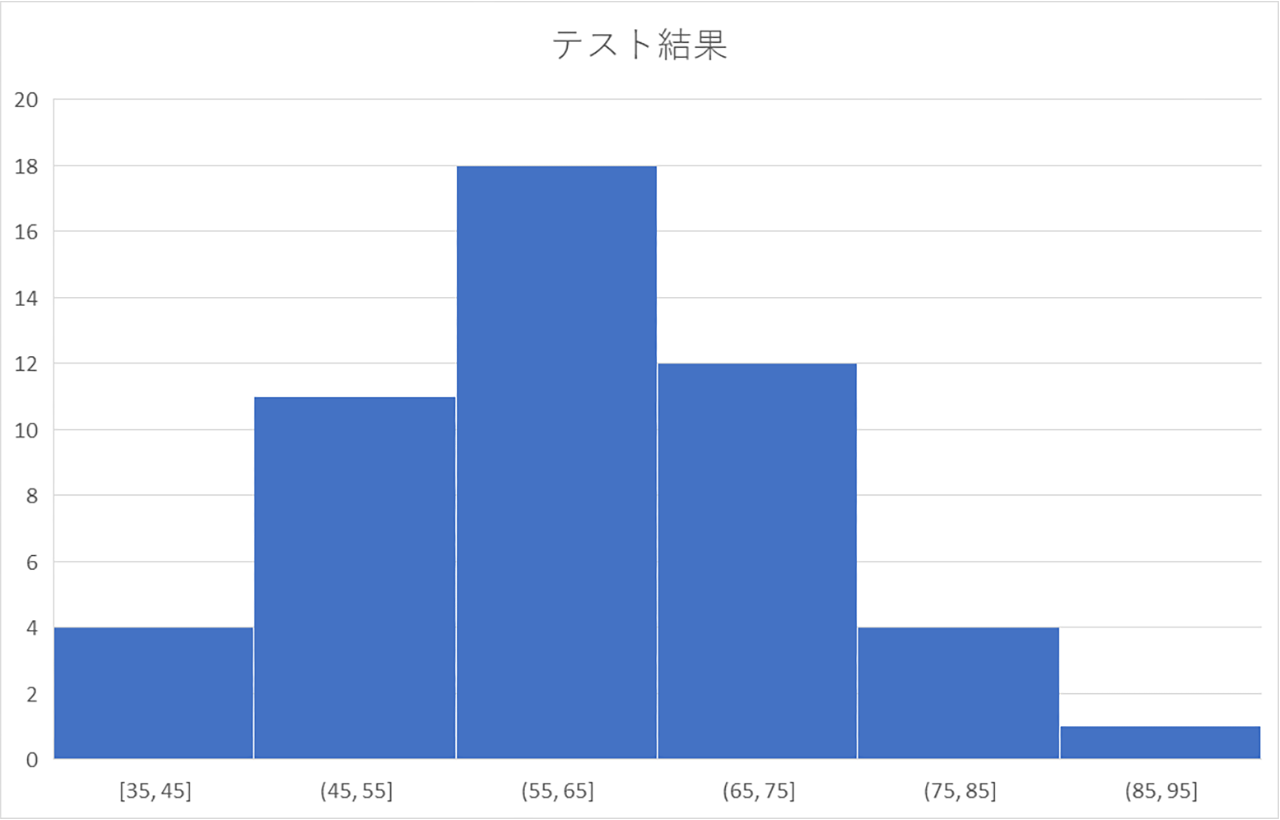
ヒストグラム

ヒストグラムとは、度数どすう分布ぶんぷ表ひょうをグラフ化したものです。これにより、直感的ちょっかんてきに傾向けいこうがわかります。

刈り込み平均値へいきんち

刈り込み平均値へいきんちとは、データの傾向けいこうをみるための方法ほうほうのひとつです。

極端きょくたんに大きなおおきな値あたいと、極端きょくたんに小さなちいさな値あたいを割合わりあい（0〜1）で除外じょがいして平均値へいきんちを求めます。

90、81、80、78、77、75、74、73、72、71、70、69、68、68、67、66、66、65、65、64、63、63、62、62、61、61、60、60、59、59、58、58、57、57、56、55、55、54、54、53、52、51、50、49、48、46、45、43、40、35

Excelでは刈り込み平均値へいきんちを計算けいさんするのにTRIMMEAN関数かんすうを使います。

=TRIMMEAN(範囲はんい, 割合わりあい)

例えばたとえば、上うえから5%と下したから5%（あわせて10%）の極端きょくたんなデータを刈り込むこむ場合ばあい、「=TREMMEAN(範囲はんい, 0.1)」と記述きじゅつします。

絶対値ぜったいち

絶対値ぜったいちとは、数学的すうがくてきには「数直線すうちょくせん上でじょうで原点げんてん（0）からどれだけ離れているかを表すあらわす値あたい」のことです。簡単かんたんには、数かずに付いている「＋」や「−」を無視むしして、常につねに正せいの数かずにすることです。

Excelでは絶対値ぜったいちを計算けいさんするのにABS関数かんすうを使います。

=ABS(数値すうち)

数字すうじを丸めるまるめる

問題もんだい4では「数字すうじを丸めるまるめる」ことを求められています。「数字すうじを丸めるまるめる」とは、切り捨てきりすてや切り上げきりあげ、四捨五入ししゃごにゅうによって、見やすくわかりやすいおおよその数字すうじにすることです。

切り上げきりあげ	注目ちゅうもくする位くらい未満みまんの値あたいが0ではない場合ばあい、その位くらいの数かずを1増やし、注目ちゅうもくする位くらい未満みまんの値あたいをすべて0にする
切り捨てきりすて	注目ちゅうもくする位くらい未満みまんの値あたいをすべて0にする
四捨五入ししゃごにゅう	注目ちゅうもくする位くらいの値あたいが5未満みまんなら切り捨てきりすて、5以上いじょうなら切り上げきりあげする

切り上げきりあげの例れい

• 1,740を「10の位くらいに切り上げきりあげる」と、1,740
• 1,740を「100の位くらいに切り上げきりあげる」と、1,800
• 1,740を「1,000の位くらいに切り上げきりあげる」と、2,000

切り捨てきりすての例れい

• 1,740を「10の位くらいに切り捨てきりすてる」と、1,740
• 1,740を「100の位くらいに切り捨てきりすてる」と、1,700
• 1,740を「1,000の位くらいに切り捨てきりすてる」と、1,000

四捨五入ししゃごにゅうの例れい

• 1,740を「10の位くらいに四捨五入ししゃごにゅうする」と、1,740
• 1,740を「100の位くらいに四捨五入ししゃごにゅうする」と、1,700
• 1,740を「1,000の位くらいに四捨五入ししゃごにゅうする」と、2,000

ROUND関数かんすう

教科書きょうかしょには記載きさいのない内容ないようです。

ROUND関数かんすうは、数字すうじを丸めるまるめるための関数かんすうです。

=ROUND(数字すうじ, 桁数けたすう)

第だい2引数ひきすうの桁数けたすうの考え方かんがえかた

• 整数せいすう3桁けた目め（100の位くらい）に四捨五入ししゃごにゅうする：-2
  • 例れい）ROUND(5256.345, -2)→5300
• 整数せいすう2桁けた目め（10の位くらい）に四捨五入ししゃごにゅうする：-1
  • 例れい）ROUND(5256.345, -1)→5260
• 整数せいすう1桁けた目め（1の位くらい）に四捨五入ししゃごにゅうする：0
  • 例れい）ROUND(5256.345, 0)→5256
• 小数しょうすう点てん以下いか1桁けた目め（0.1の位くらい）に四捨五入ししゃごにゅうする：1
  • 例れい）ROUND(5256.345, 1)→5256.3
• 小数しょうすう点てん以下いか2桁けた目め（0.01の位くらい）に四捨五入ししゃごにゅうする：2
  • 例れい）ROUND(5256.345, 2)→5256.35